【解説あり】Pythonで一般化線形モデル(GLM)を実装する方法

[chat face=”komatta_man2.png” name=”一般化線形モデルをPythonで実装したい人” align=”left” border=”gray” bg=”none”]一般化線形モデルをPythonで実装したいな…。

ついでに一般化線形モデルそのものについて知っておきたいな…。[/chat]

この記事では、上記のような悩みを解決していきます。

 

[jin_icon_check color=”#0071BB” size=”20px”] この記事の想定読者

想定している読者は、上記のとおりです。

 

この記事では「一般化線形モデルの解説とPythonの実装方法」を紹介していきます。

 

この記事を読めば、Pythonによる実装方法だけでなく、一般化線形モデルそのものについても分かるようになります。

 

Python : 一般化線形モデル(GLM)の実装コード

 

まずは、Pythonで一般化線形モデル(GLM)を実装するコードから見ていきましょう。

とりあえず実装してしまって、そのあとで理論を突き詰めていく方が、理解するには割と近道だったりします。

 

[jin_icon_check color=”#0071BB” size=”20px”] 使用するデータ

SIGNATEのお弁当需要予測データを使いますので、同じ環境下で動作確認したい方は、ぜひ会員登録して、データセットを取得してきてください。

ちなみに中身のデータセットは、こんな感じです。

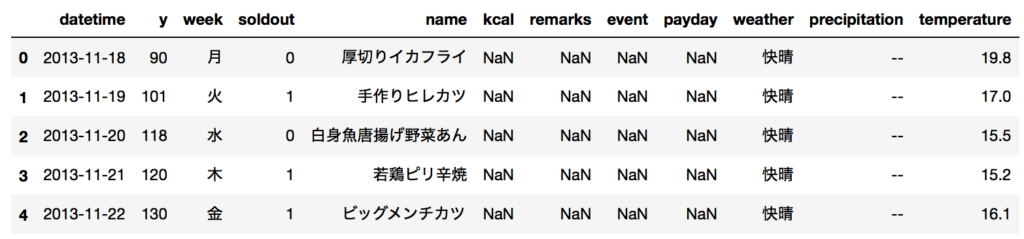
※なお、精度とかは完全に無視しています。あくまで使い方だけって感じです。

 

GLMの使い方① : とりあえずGLMを作成してみる

 

とりあえず、Pythonを使ってGLMを作成するまでを見ていきます。

statsmodelsというPythonライブラリを使うと、めちゃくちゃ簡単に書けます。

# 1. 必要なライブラリの読み込み
import pandas as pd
import statsmodels.formula.api as smf
import statsmodels.api as sm

# 2. 使用するデータの読み込み
df = pd.read_csv("train.csv")
df.head()

# 3. smf.glmで使うformula(線形予測子)とfamily(確率分布)を設定する
formula = "y ~ temperature"
family = sm.families.Poisson()

# 4. 先ほどの設定値を使って一般化線形モデルを作成
model = smf.glm(formula=formula, data=df, family=family)

# 5. 作成したモデルを学習させる
result = model.fit()

# 6. 結果の表示
result.summary()

# 7. AICを確認
result.aic

こんな感じですね。

このコードでは、一般化線形モデルの作成〜モデルの評価(AICの確認)までをおこなっています。

おそらくformulaとか意味不明かもしれませんが、そこらへんで書いている部分は、後ほど詳しく紹介していきますね。

 

GLMの使い方② : 作成したGLMを使って予測までおこなう

 

次は、作成したGLMを使って、実際に予測までやっていくコードを紹介していきます。

# 1.必要なライブラリの読み込み
import pandas as pd
import statsmodels.formula.api as smf
import statsmodels.api as sm

# 2.使用するデータの読み込み
df = pd.read_csv("train.csv")
df.head()

# 3.説明変数だけのデータセットを作成
X = df[["temperature"]]
X.head()

# 4.目的変数だけのデータセットを作成
y = df[["y"]]
y.head()

# 5.説明変数、目的変数を訓点データと評価データに分割
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.8)

# 6.smf.glmで使えるように整形
data = pd.concat([X_train, y_train], axis=1)

# 7.smf.glmで使うformula(線形予測子)とfamily(確率分布)を設定する
formula = "y ~ temperature"
family = sm.families.Poisson()

# 8.先ほどの設定値を使って一般化線形モデルを作成
model = smf.glm(formula=formula, data=data, family=family)

# 9.作成したモデルを学習させる
result = model.fit()

# 10. 結果を確認
result.summary()
result.aic

# 11.作成したモデルを使って予測する
pred = result.predict(X_test)

# 12. 実際にどのような予測がされたのか可視化する
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

%matplotlib inline
sns.set()

fig, ax = plt.subplots(figsize=(9,6))

x=np.arange(0,len(pred))

sns.scatterplot(x="temperature", y="y", data=data)
plt.plot(x, pred, color="red", lw=3)

もともとJupyter notebookで書いているものをコピペしたので、若干分かりにくいかもしれないですが、一般化線形モデルの作成〜予測結果の可視化までをおこなっています。

 

予測結果の可視化までやってみると分かりますが、かなりひどいモデルが出来上がっています…。笑

今回はもともと数字データになっていたtemperatureを使いましたが、他のデータを数値化してあげて学習してあげると、また結果が変わってきますね。

 

一般化線形モデル(GLM)とは？

 

一般化線形モデル(GLM)は、残差がどんな確率分布に従っていても、利用できるモデリング手法です。

というのも、(正規)線形モデルでは「残差が正規分布に従っていることを仮定」しています。

ただ言うまでもなく、残差が毎回のように正規分布に従っているはずもないので、一般化線形モデルを使って「残差が正規分布に従っていない場合でも、線形モデルを使えるようにした」といった感じです。

 

[jin_icon_check color=”#0071BB” size=”20px”] 一般化線形モデル3つの構成要素

一般化線形モデル(GLM)は、3つの要素で構成されています。

1つずつ見ていきましょう。

 

構成要素① : 確率分布

 

ここで言う確率分布は、「応答変数が従う確率分布」のことを指しています。

ざっくり言うと、下記のような数式の左辺Yが従う確率分布のことです。

 

[jin_icon_check color=”#0071BB” size=”20px”] よく使われる確率分布

上記のとおりです。お弁当の売り上げ個数などの離散データでは二項分布やポアソン分布を使うし、株価の値動きといった連続データには正規分布やガンマ分布を使ってあげます。

 

構成要素② : 線形予測子

 

線形予測子は、下記のような説明変数とパラメータ線型結合で表される式です。

これまたざっくり言うと、よくみる下記のような数式の右辺に該当する部分ですね。

 

構成要素③ : リンク関数

 

ただ、Y=aX+bのような式を、そのまま使おうとすると不都合が生じてきます。

たとえば、お弁当の売り上げ予測の場合だと、売り上げでマイナスになる可能性はないですよね。

でもY=aX+bのままだと直線になるので、言うまでもなくマイナスの値を取ることになります。

 

 

このモデル化のときに生じる問題を解決するのが、リンク関数Gです。数式で表すと、下記のとおり。

たとえば、G=logであれば、下記のような式になります。

そして、もともと説明してあげたかったYについての式に変換すると、下記の式になりますよね。

このように変換できれば、Yがマイナスの値を取ることはなく、もともと直線でしか表現できなかったのが、曲線で表現できるようになります。

 

[jin_icon_check color=”#0071BB” size=”20px”] 確率分布によって、だいたいリンク関数が決まっている件

さらに、リンク関数は、応答変数が従う確率分布によって、あらかた決まっています。

Y ~ 確率分布	リンク関数G(Y)
二項分布	ロジット関数
ポアソン分布	log(対数関数)
ガンマ分布	log(対数関数), ガンマ関数
正規分布	恒等関数

上記のとおりですね。

なので、確率分布が決まってくれば、必然的に使用するリンク関数も決まってくる感じです。

 

補足 : 一般化線形モデルの構成要素とstatsmodelsの対応

 

ここまで読んでいたら分かったかもですが、一般化線形モデルの実装に使っていたstatsmodelsとの対応関係を見ておきたいと思います。

 

[jin_icon_check color=”#0071BB” size=”20px”] 元のソースコード

# 1. 必要なライブラリの読み込み
import pandas as pd
import statsmodels.formula.api as smf
import statsmodels.api as sm

# 2. 使用するデータの読み込み
df = pd.read_csv("train.csv")
df.head()

# 3. smf.glmで使うformula(線形予測子)とfamily(確率分布)を設定する
formula = "y ~ temperature"
family = sm.families.Poisson()

# 4. 先ほどの設定値を使って一般化線形モデルを作成
model = smf.glm(formula=formula, data=df, family=family)

# 5. 作成したモデルを学習させる
result = model.fit()

# 6. 結果の表示
result.summary()

# 7. AICを確認
result.aic

 

GLMの構成要素	statsmodelsの対応部分
確率分布	family
線形予測子	formula
リンク関数	sm.families.Poisson(link)

上記のとおりです。リンク関数はポアソン分布の場合、デフォルトで対数関数に設定されているため、今回は記述しませんでした。

もし、別途リンク関数を設定してあげるなら、確率分布の引数に渡してあげましょう。

 

それでは、この辺でおしまいにします。

 

[jin_icon_check color=”#0071BB” size=”20px”] 線形モデルの学習でおすすめの本

 

[jin_icon_check color=”#0071BB” size=”20px”] おすすめの記事